Công thức tính độ dài đường trung tuyến

Cách tính phỏng lâu năm lối trung tuyến vô tam giác

Trong nội dung bài viết này VnDoc tiếp tục tổ hợp lại kỹ năng và kiến thức về lối trung tuyến vô tam giác và công thức tính phỏng lâu năm lối trung tuyến vô tam giác, mời mọc những em học viên nằm trong tìm hiểu thêm.

Bạn đang xem: Công thức tính độ dài đường trung tuyến

Trong công tác Toán 7 môn Hình học tập học kì 2 với chuyên mục Tính hóa học 3 lối trung tuyến của tam giác. Để canh ty những em học viên tóm dĩ nhiên kỹ năng và kiến thức về nội dung này, VnDoc trình làng cho tới những em bao quát lý thuyết và một vài bài xích tập luyện áp dụng với đáp án, gần giống bài xích tập luyện cho những em tự động luyện nhằm ôn tập luyện và gia tăng kỹ năng và kiến thức được học tập bên trên lớp gần giống vô SGK Toán 7 tập luyện 2.

Để tiện trao thay đổi, share tay nghề về giảng dạy dỗ và tiếp thu kiến thức những môn học tập lớp 7, VnDoc mời mọc những thầy gia sư, những bậc cha mẹ và chúng ta học viên truy vấn group riêng rẽ dành riêng cho lớp 7 sau: Nhóm Tài liệu tiếp thu kiến thức lớp 7. Rất ước cảm nhận được sự cỗ vũ của những thầy cô và chúng ta.

Định nghĩa lối trung tuyến

- Đường trung tuyến của một quãng trực tiếp là 1 đường thẳng liền mạch trải qua trung điểm của đoạn trực tiếp bại liệt.

Định nghĩa lối trung tuyến của tam giác

- Đường trung tuyến của một tam giác là đoạn trực tiếp nối kể từ đỉnh của tam giác cho tới trung điểm của cạnh đối lập vô hình học tập phẳng phiu. Mỗi tam giác với 3 lối trung tuyến.

Đường trung tuyến của tam giác

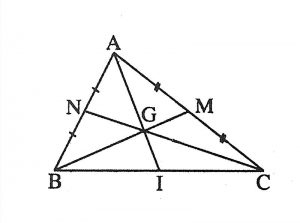
Theo như hình vẽ bên trên thì những đoạn trực tiếp AI, công nhân, BM được xem là 3 trung tuyến của tam giác ABC.

Tính hóa học của lối trung tuyến vô tam giác

- Ba lối trung tuyến của tam giác nằm trong trải qua một điểm. Điểm bại liệt cơ hội đỉnh một khoảng chừng bởi vì 2/3 phỏng lâu năm lối trung tuyến trải qua đỉnh ấy.

Giao điểm của tía lối trung tuyến gọi là trọng tâm.

Ví dụ:

Gọi G là trọng tâm của tam giác ABC, ABC với những trung tuyến AI, BM, công nhân thì tớ sẽ có được biểu thức:

Định nghĩa lối trung tuyến vô tam giác vuông

- Tam giác vuông là 1 tình huống đặc biệt quan trọng của tam giác, vô bại liệt, tam giác sẽ có được một góc có tính rộng lớn là 90 phỏng, và nhì cạnh tạo thành góc này vuông góc cùng nhau.

- Do bại liệt, lối trung tuyến của tam giác vuông sẽ có được không thiếu thốn những đặc điểm của một lối trung tuyến tam giác.

Định lý 1: Trong một tam giác vuông, lối trung tuyến ứng với cạnh huyền bởi vì nửa cạnh huyền.

Định lý 2: Một tam giác với trung tuyến ứng với cùng một cạnh bởi vì nửa cạnh bại liệt thì tam giác ấy là tam giác vuông.

Ví dụ:

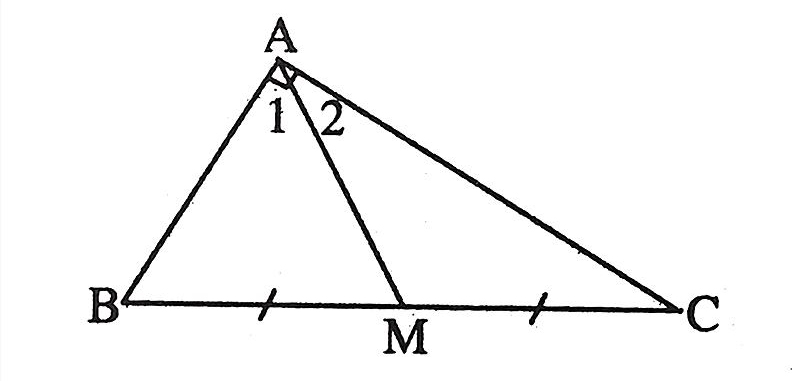
Tam giác ABC vuông ở A, phỏng lâu năm lối trung tuyến AM tiếp tục bởi vì MB, MC và bởi vì một nửa BC

Ngược lại nếu như AM = một nửa BC thì tam giác ABC tiếp tục vuông ở A.

Các bài xích tập luyện tự động luyện:

Bài 1: Cho tam giác ABC cân nặng ở A có AB = AC = 17cm, BC= 16cm. Kẻ trung tuyến AM.

a) Chứng minh: AM ⊥ BC;

b) Tính độ dài AM.

Hướng dẫn giải

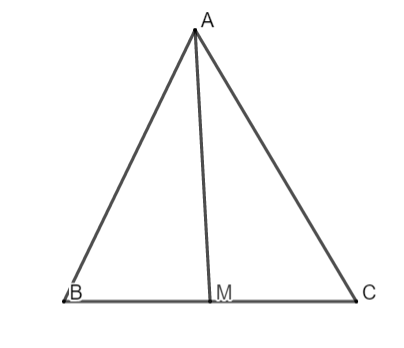
a. Ta với AM là lối trung tuyến tam giác ABC nên MB = MC

Mặt không giống tam giác ABC là tam giác cân nặng bên trên A

Suy đi ra AM một vừa hai phải là lối trung tuyến một vừa hai phải là lối cao

Vậy AM vuông góc với BC

b. Ta có

BC = 16cm nên BM = MC = 8cm

AB = AC = 17cm

Xét tam giác AMC vuông bên trên M

Áp dụng tấp tểnh lý Pitago tớ có:

AC² = AM² + MC² ⇒ 17² = AM² + 8² ⇒ AM² = 17² - 8² = 225 ⇒ AM = 15cm

Bài 2: Cho G là trọng tâm của tam giác đều ABC. Chứng minh rằng GA = GB = GC.

Hướng dẫn giải

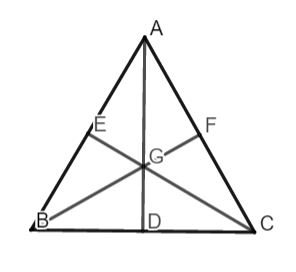
Gọi AD, CE, BF là những lối trung tuyến tam giác ABC hoặc D, E, F theo lần lượt là trung điểm cạnh BC, AB, AC

Ta với AD là lối trung tuyến tam giác ABC nên (1)

CE là lối trung tuyến tam giác ABC nên (2)

BF là lối trung tuyến tam giác ABC nên (3)

Ta với tam giác BAC đều nên đơn giản dễ dàng suy đi ra AD = BF = CE (4)

Từ 1, 2, 3, 4 suy đi ra AG = BG = CG

Bài 3: Cho tam giác ABC. Trên tia đối của tia AB lấy điểm D sao cho tới AD = AB. Trên cạnh AC lấy điểm E sao cho tới AE = 1/3AC. Tia BE tách CD ở M. Chứng minh :

a) M là trung điểm của CD

b) AM = BC.

Hướng dẫn giải

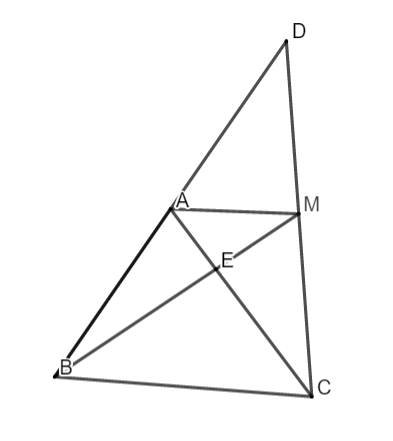
a. Xét tam giác BDC với AB = AD suy đi ra AC là lối trung tuyến tam giác BCD

Mặt khác

Suy đi ra E là trọng tâm tam giác BCD

M là phú của BE và CD

Vậy BM là trung tuyến tam giác BCD

Vậy M là trung điểm của CD

b. A là trung điểm của BD

M là trung điểm của DC

Suy đi ra AM là lối tầm của tam giác BDC

Suy đi ra AM = một nửa BC

Bài 4: Cho tam giác ABC, trung tuyến BM. Trên tia BM lấy nhì điểm G và K sao cho tới BG = BM và G là trung điểm của BK. Gọi N là trung điểm của KC , GN tách CM ở O. Chứng minh:

a) O là trọng tâm của tam giác GKC ;

b) GO = BC

Học sinh tự động giải

Bài 5: Cho tam giác ABC vuông ở A, với AB = 18cm, AC = 24cm. Tính tổng những khoảng cách kể từ trọng tâm G của tam giác cho tới những đỉnh của tam giác.

Hướng dẫn giải

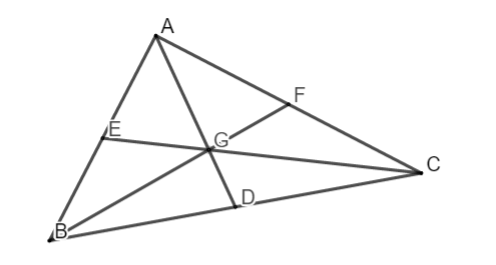
Gọi AD, CE, BF theo lần lượt là những lối trung tuyến nối kể từ đỉnh A, C, B của tam giác ABC

Dễ dàng suy đi ra AE = EB = 9cm, AF = FC = 12cm

Ta với tam giác ABC vuông bên trên A, vận dụng tấp tểnh lý Pitago tớ có:

BC² = AB² + AC² ⇒ BC² = 18² + 24² = 900 ⇒ BC = 30cm

Ta với ABC vuông nhưng mà D là trung điểm cạnh huyền nên AD = BD = DC = 15cm

Suy ra: AG = 2/3 AD = 10cm

Xem thêm: Vé máy bay Hà Nội Đảo Phú Quốc giá rẻ | Trip.com

Xét tam giác AEC vuông bên trên A, vận dụng tấp tểnh lý Pitago tớ có:

EC² = AE² + AC² ⇒ EC² = 9² + 24² = 657 ⇒ EC = 3√73 centimet ⇒ CG = 2/3 EC = 2√73 cm

Tương tự động tớ xét tam giác AFB vuông bên trên A, vận dụng tấp tểnh lý Pitago tớ có:

BF² = AB² + AF² ⇒BF² = 18² + 12² = 468 ⇒ BF = 6√13 centimet ⇒ BG = 2/3 BF = 4√13 cm 

Tổng những khoảng cách kể từ trọng tâm G của tam giác cho tới những đỉnh của tam giác là:

AG + BG + CG = 10 + 4√13 + 2√73 (cm)

Bài 6: Cho tam giác ABC, trung tuyến AM. tường AM = BC. Chứng minh rằng tam giác ABC vuông ở A.

Học sinh tự động giải

Bài 7: Cho tam giác ABC. Các lối trung tuyến BD và CE. Chứng minh

Hướng dẫn giải

Học sinh tự động vẽ hình.

Xét tam giác BGC có:

BG + CG > BC

⇒

⇒ BD + CE >

Bài 8: Cho tam giác ABC cân nặng bên trên A, hai tuyến phố trung tuyến BD và CE tách nhau bên trên G. Kéo lâu năm AG tách BC bên trên H.

a. So sánh tam giác AHB và tam giác AHC.

b. Gọi I và K theo lần lượt là trung điểm của GA và GC. Chứng minh rằng AK, BD, CI đồng quy.

Hướng dẫn giải

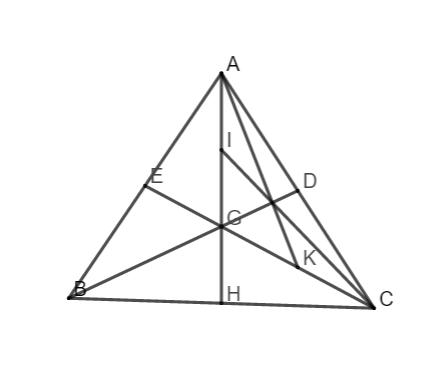
a. Ta với BD là lối trung tuyến của tam giác ABC

CE là lối trung tuyến của tam giác ABC

Vậy G là trọng tâm tam giác ABC

Mà AH trải qua G nên AH là lối trung tuyến của tam giác ABC

HB = HC

Xét nhì tam giác AHB và tam giác AHC có:

AB = AC (tam giác ABC cân nặng bên trên A)

AH chung

HB = HC

⇒ ΔAHB = ΔAHC (c - c - c)

b. Ta với IA = IG nên CI là lối trung tuyến của tam giác AGC (1)

Ta lại sở hữu KG = KC nên AK là lối trung tuyến của tam giác AGC (2)

DG là lối trung tuyến của tam giác AGC (3)

Từ (1), (2), (3) suy đi ra 3 lối trung tuyến CI, AK, DG đồng quy bên trên I

Bài 9: Cho tam giác ABC với AB = AC, gọi K là phú điểm của hai tuyến phố trung tuyến BM và công nhân. Chứng minh rằng:

a. Tam giác BNC và tam giác CMB bởi vì nhau

b. KB = KC

c. BC < 4KM

Hướng dẫn giải

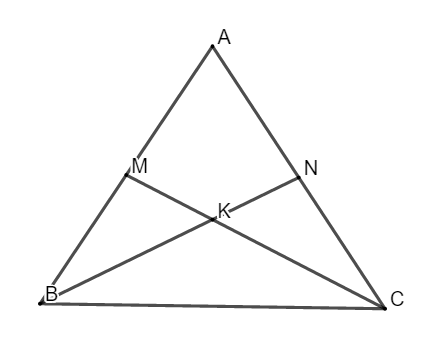
a. Ta có: AB = AC (gt)

BM là lối trung tuyến của tam giác ABC

CN là lối trung tuyến của tam giác ABC

⇒ BN = CM

Xét ΔBCN và ΔCBM có:

BC là cạnh chung

BN = CM

 (tam giác ABC cân nặng bên trên A)

⇒ ΔBNC = ΔCMB (c - g - c)

b. Ta có: ( Vì ΔBNC = ΔCMB)

Nên tam giác KBC cân nặng bên trên A

Suy đi ra KB = KC

c. Xét ΔABC có:

NA = NB (CN là lối trung tuyến)

MA = MC (MB là lối trung tuyến)

Suy đi ra NM là lối tầm của tam giác ABC

Xét tam giác NKM có:

NM < NK + KM (bất đẳng thức Cauchy vô tam giác)

NK = công nhân – CK

⇒ BC/2 < công nhân - CK + KM (1)

ΔBNC = ΔCMB ⇒ công nhân = BM (2)

Tam giác KBC cân nặng tai K ⇒ CK = BK (3)

Từ (1), (2), (3) ⇒ BC/2 < BM - BK + KM

⇒ BC/2 < 2KM

⇒ BC < 4KM

(Còn tiếp)

Mời độc giả chuyển vận tư liệu tìm hiểu thêm lênh láng đủ!

Xem thêm: Ý nghĩa quan trọng nhất của việc hoàn thành thống nhất đất nước về mặt nhà

----------------------------------------------------

Trên phía trên, VnDoc tiếp tục trình làng cho tới thầy cô và những em học viên tư liệu Công thức tính phỏng lâu năm lối trung tuyến. Trong khi, mời mọc chúng ta tìm hiểu thêm thêm thắt những tư liệu môn Toán 7 không giống như: Giải bài xích tập luyện Toán lớp 7, Giải Vở BT Toán 7, Đề đua học tập kì 1 lớp 7, Đề đua thân thuộc kì 1 lớp 7, Đề đua học tập kì 2 lớp 7... cũng khá được update liên tiếp bên trên VnDoc.com.

Một số tư liệu tìm hiểu thêm tương quan cho tới bài xích học: