1. Lý thuyết:
\(V=\frac{1}{3}.\pi .R^{2}.h\)
\((=\frac{1}{3}.S_{day}.h)\)
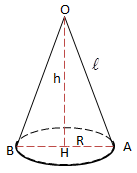
R: nửa đường kính hình tròn trụ đáy
h: độ cao ( khoảng cách kể từ đỉnh cho tới đáy)
2. Bài tập:
Ví dụ 1: Cho khối nón có tính lâu năm lối sinh bởi vì 5cm, nửa đường kính hình tròn trụ lòng là 3cm. Tính thể tích khối nón.
\(\left\{\begin{matrix} l=5cm\\R=3cm \end{matrix}\right.\)
Giải:
Gọi O là đỉnh khối nón
H là tâm hình tròn
A là vấn đề nằm trong lối tròn trặn đáy
OA=5cm, HA=3cm
Trong tam giác vuông OHA,
\(OH=\sqrt{OA^{2}-HA^{2}}=\sqrt{5^{2}-3^{2}}=4\)
\(V=\frac{1}{3}\pi .R^{2}.h=\frac{1}{3}\pi .3^{2}.4=12\pi (cm^{3})\)
Ví dụ 2: Cho khối nón sở hữu góc ở đỉnh bằng \(60^{\circ}\) độ lâu năm lối sinh bởi vì 6cm. Tính thể tích khối nón.
Giải:
Gọi O là đỉnh khối nón. Kẻ 2 lần bán kính AB của hình tròn trụ lòng tâm H.
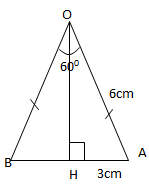
Theo bài bác đi ra,
\(\widehat{AOB}=60^{\circ},\hspace{3}OA=OB=6(cm)\)
Suy đi ra, \(\Delta OAB\) đều nên AB=6cm
\(\Rightarrow R=HA=3(cm)\)
Trong tam giác vuông OHA, \(\widehat{AOH}=30^{\circ}\)
\(OH=OA.\cos30^{\circ}=6.\frac{\sqrt{3}}{2}=3\sqrt{3}(cm)\)
\(V=\frac{1}{3}.\pi .3^{2}.3\sqrt{3}=9\pi \sqrt{3}(cm^{3})\)
Chú ý: \(OH=\sqrt{OA^{2}-HA^{2}}=\sqrt{6^{2}-3^{2}}=3\sqrt{3}\) hoặc \(OH=HA.\cot30^{\circ}=3\sqrt{3}\)
Bạn đang xem: Bài 2: Thể tích khối nón
Ví dụ 3: Cho \(\Delta ABC\) vuông bên trên A, AB=8(cm), BC=10(cm). Tính thể tích khối tròn trặn xoay tạo ra trở nên khi mang đến lối bộp chộp khúc
a) Ngân Hàng Á Châu ACB xoay quanh AB.
b) ABC xoay quanh AC.
a) BAC xoay quanh BC.Giải:
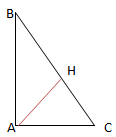
Trong tam giác vuông ABC,
\(AC=\sqrt{BC^{2}-AB^{2}}=\sqrt{10^{2}-8^{2}}=6(cm)\)
a) Khi đường bộp chộp khúc ACB xoay quanh AB tớ được hình nón sở hữu độ cao h=AB=8(cm), nửa đường kính R=AC=6(cm).
\(V=\frac{1}{3}.\pi .R^{2}.h=\frac{1}{3}.\pi .6^{2}.8=96\pi (cm^{3})\)
b) Khi đường bộp chộp khúc ABC xoay quanh AC tớ được hình nón sở hữu độ cao h=AC=6(cm), nửa đường kính R=AB=8(cm).
\(V=\frac{1}{3}.\pi .R^{2}.h=\frac{1}{3}.\pi .8^{2}.6=128\pi (cm^{3})\)
c) Khi đường bộp chộp khúc BAC xoay quanh BC tớ được 2 hình nón.
+ Hình nón loại nhất tạo ra trở nên khi mang đến lối bộp chộp khúc BAH xoay quanh BH
R1=AH, h1=BH.
Trong tam giác vuông ABC:
\(\frac{1}{AH^{2}}=\frac{1}{AB^{2}}+\frac{1}{AC^{2}}=\frac{1}{8^{2}}+\frac{1}{6^{2}}=\frac{10^{2}}{8^{2}.6^{2}}\)
\(\Rightarrow R_{1}=AH=\frac{8.6}{10}=\frac{24}{5}\)
\(h_{1}=BH=\sqrt{AB^{2}-AH^{2}}=\sqrt{8^{2}-\frac{8^{2}.6^{2}}{10^{2}}}=8\sqrt{\frac{10^{2}-6^{2}}{10^{2}}}=\frac{8^{2}}{10}=\frac{32}{5}\)\(V_{1}=\frac{1}{3}.\pi .R_{1}^{2}.h_{1}=\frac{1}{3}.\pi .\frac{48^{2}}{10^{2}}.\frac{32}{5}=\frac{6144}{125}(cm^{3})\)
+ Hình nón loại nhị tọa trở nên khi mang đến lối bộp chộp khúc HAC xoay quanh HC.
\(\Rightarrow R_{1}=AH=\frac{24}{5}\)
\(h_{2}=HC=BC-HB=10-\frac{32}{5}=\frac{18}{5}\)
\(V_{2}=\frac{1}{3}.\pi .R_{2}^{2}.h_{2}=\frac{1}{3}.\pi .\frac{24^{2}}{5^{2}}.\frac{18}{5}=\frac{3456}{125}(cm^{3})\)
\(V=V_{1}+V_{2}=\frac{384}{5}(cm^{3})\)
Cách 2: \(V=V_{1}+V_{2}=\frac{1}{3}\pi R_{1}^{2}.h_{1}+\frac{1}{3}\pi R_{2}^{2}.h_{2}\)
\(=\frac{1}{3}\pi R_{1}^{2}.(h_{1}+h_{2})=\frac{1}{3}\pi .\frac{24^{2}}{5^{2}}(\frac{32}{5}+\frac{18}{5}) =\frac{1}{3}\pi .\frac{24^{2}}{5^{2}}.10\)
Nhận xét:
\(V=\frac{1}{3}\pi .AH^{2}.BC=\frac{1}{3}\pi .AH.\frac{AB^{2}.AC^{2}}{AB^{2}+AC^{2}}.BC\)